Chapter 0. Randomness
“The generation of random numbers is too important to be left to chance.”
— Robert R. Coveyou
Here we are: the beginning. If it’s been a while since you’ve programmed in JavaScript (or done any math, for that matter), this chapter will reacquaint your mind with computational thinking. To start your coding of nature journey, I’ll introduce you to some foundational tools for programming simulations: random numbers, random distributions, and noise. Think of this as the first (zeroth!) element of the array that makes up this book—a refresher and a gateway to the possibilities that lie ahead.
In Chapter 1, I’m going to talk about the concept of a vector and how it will serve as the building block for simulating motion throughout this book. But before I take that step, let’s think about what it means for something to move around a digital canvas. I’ll begin with one of the best-known and simplest simulations of motion: the random walk.

Random Walks
Imagine you’re standing in the middle of a balance beam. Every ten seconds, you flip a coin. Heads, take a step forward. Tails, take a step backward. This is a random walk, a path defined as a series of random steps. Stepping (carefully) off that balance beam and onto the floor, you could perform a random walk in two dimensions by flipping the same coin twice with the following results:
| Flip 1 | Flip 2 | Result |
|---|---|---|
| Heads | Heads | Step forward. |
| Heads | Tails | Step right. |
| Tails | Heads | Step left. |
| Tails | Tails | Step backward. |
This may seem like an unsophisticated algorithm, but you can use random walks to model all sorts of phenomena that occur in the real world, from the movements of molecules in a gas, to an animal foraging for food, to the behavior of a gambler spending a day at the casino. For our purposes, the random walk is the perfect place to start for three reasons:
- I’d like to review a programming concept central to this book: object-oriented programming. The random walker I’m about to create will serve as a template for how I’ll use object-oriented design to make things that move around a computer graphics canvas.
- The random walk instigates the two questions that I’ll ask over and over again throughout this book: “How do you define the rules that govern the behavior of your objects?” and then, “How do you implement these rules in code?”
- You’ll periodically need a basic understanding of randomness, probability, and Perlin noise for this book’s projects. The random walk will allow me to demonstrate key points that will come in handy later.
I’ll first review a bit of object-oriented programming (OOP) by coding a Walker class to create Walkerobjects that can go for a random walk. This will only be a cursory review. If you’ve never worked with OOP before, you may want something more comprehensive; I’d suggest stopping here and reviewing this video tutorial on the basics of ES6 classes with p5.js before continuing.
The Random Walker Class
An object in JavaScript is an entity that has both data and functionality. In this case, a Walker object should have data about its position on the canvas and functionality such as the capability to draw itself or take a step.
A class is the template for building actual instances of objects. Think of a class as the cookie cutter and objects as the cookies themselves. To create a Walker object, I’ll begin by defining the Walker class—what it means to be a Walker.
The Walker only needs two pieces of data: a number for its x-position and one for its y-position. I’ll initialized them to the center of the canvas to set the object’s starting position. I can do this in the class’s constructor function, appropriately named constructor(). You can think of the constructor as the object’s setup() function. It’s responsible for defining the initial properties of an object, much like setup() does for the entire sketch.
constructor() {
Objects have a constructor where they are initialized.
this.x = width / 2;
this.y = height / 2;
}
Objects have data.
Notice the use of the keyword this to attach the properties to the newly created object itself: this.x and this.y.
In addition to data, classes can be defined with functionality. In this example, a Walker object has two functions, known as methods in an OOP context. While methods are essentially functions, the distinction is that methods are defined inside of a class, and so are associated with an object or class, whereas functions aren’t. The function keyword is a nice clue: you'll see it when defining standalone functions, but it won’t appear inside a class. I’ll try my best to use the terms consistently in this book, but it’s common for programmers to use the terms “function” and “method” interchangeably.
The first method, show(), includes the code to draw the object (as a black dot). Once again, never forget the this. when referencing the properties (variables) of that object.
show() {
stroke(0);
point(this.x, this.y);
}
Objects have methods.
The next method, step(), directs the Walker object to take a step. This is where things get a bit more interesting. Remember taking steps in random directions on a floor? Now I’ll use a p5.js canvas to represent that floor. There are four possible steps. A step to the right can be simulated by incrementing x with x++; to the left by decrementing x with x--; forward by going up a pixel (y--); and backward by going down a pixel (y++). But how can the code pick from these four choices?
Earlier I stated that you could flip two coins. In p5.js, however, when you want to randomly choose from a list of options, you can simply generate a random number with the random() function. It picks a random floating point (decimal) value within any range you want.
let choice = floor(random(4));
Here I declare a variable choice and assign it a random integer (whole number) with a value of 0, 1, 2, or 3 by removing the decimal places from the random floating point number using floor(). Technically speaking, the number picked by calling random(4) can never be 4.0, since the top end of the range isn’t inclusive. Rather, the highest possibility is 3.999999999 (with as many 9s as JavaScript will allow), which floor() will round down to 3.
Declaring Variables
In JavaScript, variables can be declared using either let or const. A typical approach would be to declare all variables with const and change to let when needed. In this first example, const would be appropriate for declaring choice as it’s never reassigned a new value over the course of its life inside each call to step(). While this differentiation is important, I’m choosing to follow the p5.js example convention and declare all variables with let. I recognize there are important reasons for having const and let. However, the distinction can be a distraction and confusing for beginners. I encourage you, the reader, to explore the topic further and make your own decisions about how to best declare variables in your own sketches. For more, you can read the discussion surrounding issue #3877 in the p5.js GitHub repository.
While I'm at it, I'm also choosing to use the "strict" equality boolean operator in JavaScript: ===. This operator tests both value and type equality. For example, 3 === '3' will evaluate to false because the types are different (number vs. string), even though they look similar. On the other hand, using == in 3 == '3' will result in true because the two different types are converted to be comparable, which can sometimes lead to unexpected results. Although the loose comparison == would work fine here, === is probably a safer option.
Next, the walker takes the appropriate step (left, right, up, or down), depending on which random number was picked. Here’s the full step() method closing out the Walker class.
step() {
let choice = floor(random(4));
0, 1, 2, or 3
if (choice === 0) {
this.x++;
} else if (choice === 1) {
this.x--;
} else if (choice === 2) {
this.y++;
} else {
this.y--;
}
}
}
The random "choice" determines the step.
Now that I’ve written the class, it’s time to make an actual Walker object in the sketch itself. Assuming you’re looking to model a single random walk, start with a single global variable.
let walker;
A Walker object
Then create the object in setup() by referencing the class name with the new operator.
function setup() {
Remember how p5.js works? setup() is executed once when the sketch starts...
createCanvas(640, 240);
walker = new Walker();
background(255);
}
Create the Walker.
Finally, during each cycle through draw(), the Walker takes a step and draws a dot.
function draw() {
...and draw() loops forever and ever (until you quit).
walker.step();
walker.show();
}
Call functions on the Walker.
Since the background is drawn once in setup(), rather than clearing it continually each time through draw(), the trail of the random walk is visible in the canvas.
Example 0.1: A Traditional Random Walk
There are a couple adjustments I could make to the random walker. For one, this Walker object’s steps are limited to four options: up, down, left, and right. But any given pixel in the canvas can be considered to have eight possible neighbors, including diagonals (see Figure 0.1). A ninth possibility to stay in the same place could also be an option.
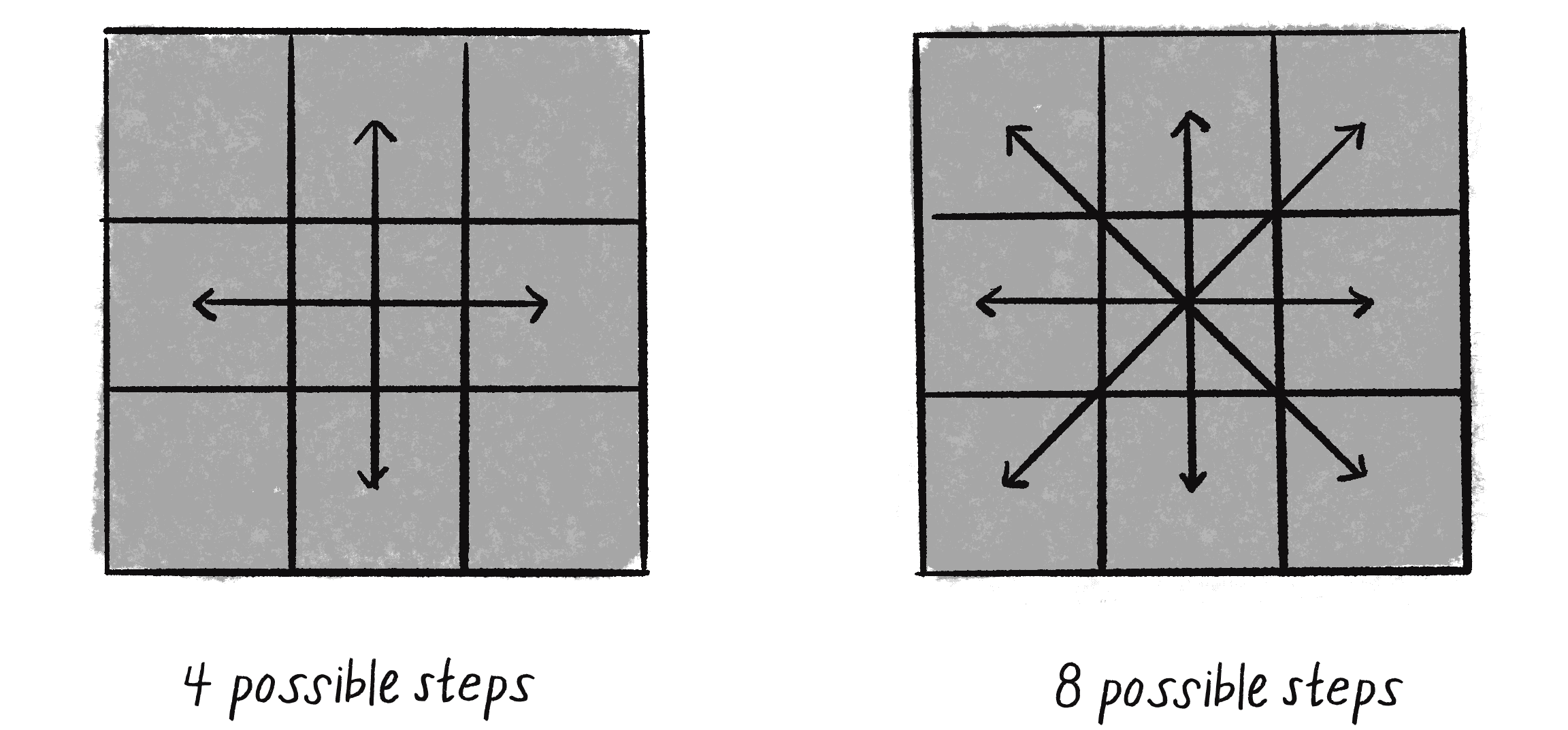
To implement a Walker object that can step to any neighboring pixel (or stay put), I could pick a number between 0 and 8 (nine possible choices). However, another way to write the code would be to pick from three possible steps along the x-axis (-1, 0, or 1) and three possible steps along the y-axis.
step() {
let xstep = floor(random(3)) - 1;
let ystep = floor(random(3)) - 1;
Yields -1, 0, or 1
this.x += xstep;
this.y += ystep;
}
Taking this further, I could get rid of floor() and use the random() function’s original floating point numbers to create a continuous range of possible step lengths between -1 and 1.
step() {
let xstep = random(-1, 1);
let ystep = random(-1, 1);
Any floating point number between -1.0 and 1.0
this.x += xstep;
this.y += ystep;
}
All of these variations on the “traditional” random walk have one thing in common: at any moment in time, the probability that the Walker will take a step in a given direction is equal to the probability that the Walker will take a step in any other direction. In other words, if there are four possible steps, there is a 1 in 4 (or 25 percent) chance the Walker will take any given step. With nine possible steps, it’s a 1 in 9 chance (about 11.1 percent).
Conveniently, this is how the random() function works. p5’s random number generator (which operates behind the scenes) produces a uniform distribution of numbers. You can test this distribution with a sketch that counts each time a random number is picked and graphs it as the height of a rectangle.
Example 0.2: A Random Number Distribution
let randomCounts = [];
An array to keep track of how often random numbers are picked
let total = 20;
function setup() {
createCanvas(640, 240);
for (let i = 0; i < total; i++) {
randomCounts[i] = 0;
}
}
function draw() {
background(255);
Total number of slots
let index = floor(random(randomCounts.length));
randomCounts[index]++;
stroke(0);
fill(127);
let w = width / randomCounts.length;
Pick a random number and increase the count.
for (let x = 0; x < randomCounts.length; x++) {
rect(x * w, height - randomCounts[x], w - 1, randomCounts[x]);
}
}
Graphing the results
Notice how each bar of the graph differs slightly in height. The sample size (the number of random numbers picked) is small, so occasional discrepancies where certain numbers are picked more often emerge. Over time, with a good random number generator, this would even out.
Pseudorandom Numbers
The random numbers from the random() function aren’t truly random; instead, they’re known as pseudorandom because they’re the result of a mathematical function that merely simulates randomness. This function would yield a pattern over time, and thus stop seeming to be random. That time period is so long, however, that random() is random enough for the examples in this book.
Exercise 0.1
Create a random walker that has a greater tendency to move down and to the right. (The solution follows in the next section.)
Probability and Nonuniform Distributions
Uniform randomness often isn’t the most thoughtful solution to a design problem—in particular, the kind of problem that involves building an organic or natural-looking simulation. With a few tricks, however, the random() function can instead produce nonuniform distributions of random numbers, where some outcomes are more likely than others. This can yield more interesting, seemingly natural results.
Think about when you first started programming with p5.js. Perhaps you wanted to draw a lot of circles on the screen, so you said to yourself, “Oh, I know! I’ll draw all these circles at random positions, with random sizes and random colors.” Seeding a system with randomness is a perfectly reasonable starting point when you’re learning the basics of computer graphics, but in this book, I’m looking to build systems modeled on what we see in nature, and uniform randomness won’t always cut it. Sometimes you have to put your thumb on the scales a little bit.
Creating a nonuniform distribution of random numbers will come in handy throughout the book. In Chapter 9’s genetic algorithms, for example, I’ll need a methodology for performing “selection”—which members of the population should be selected to pass their DNA to the next generation? This is akin to the Darwinian concept of “survival of the fittest.” Say you have an evolving population of monkeys. Not every monkey has an equal chance of reproducing. To simulate Darwinian natural selection, you can’t simply pick two random monkeys to be parents. The more “fit” ones should be more likely to be chosen. This could be considered the “probability of the fittest.”
Let me pause here and take a look at probability’s basic principles, so I can apply more precise words to the coding examples to come. I’ll start with single-event probability—the likelihood that a given event will occur. In probability, outcomes refer to all the possible results of a random process, and an event is the specific outcome or combination of outcomes being considered.
If you have a scenario where each outcome is just as likely as the others, the probability of given event occurring equals the number of outcomes that match that event divided by the total number of all potential outcomes. A coin toss is a simple example: it has only two possible outcomes, heads or tails. There’s only one way to flip heads, so the probability that the coin will turn up heads is one divided by two: 1/2, or 50 percent.
Take a deck of 52 cards. The probability of drawing an ace from that deck is:
The probability of drawing a diamond is:
You can also calculate the probability of multiple events occurring in sequence by multiplying the individual probabilities of each event. For example, the probability of a coin turning up heads three times in a row is:
This indicates a coin will turn up heads three times in a row one out of eight times on average. If you flipped a coin three times in a row 500 times, you would expect to see an outcome of three consecutive heads an average of one-eighth of the time, or about 63 times.
Exercise 0.2
What is the probability of drawing two aces in a row from a deck of 52 cards, if you reshuffle your first draw back into the deck before making your second draw? What would that probability be if you didn’t reshuffle after your first draw?
There are a couple of ways to use the random() function to apply the concepts of probability in your code for a nonuniform distribution. One technique is to fill an array with numbers—some of which are repeated—then choose random elements from that array and generate events based on those choices.
let stuff = [1, 1, 2, 3, 3];
1 and 3 are stored in the array twice, making them more likely to be picked than 2.
let value = random(stuff);
Picking a random element from an array
print(value);
The five-member array has two 1s, so running this code will produce a 2/5 = 40 percent chance of printing the value 1. Likewise, there’s a 20 percent chance of printing 2, and a 40 percent chance of printing 3.
You can also ask for a random number (let’s make it simple and just consider random floating point values between 0 and 1) and allow an event to occur only if the random number is within a certain range. For example:
let probability = 0.1;
A probability of 10%
let r = random(1);
A random floating point between 0 and 1
if (r < probability) {
print('Sing!');
}
If the random number is less than 0.1, sing!
One-tenth of the floating point numbers between 0 and 1 are less than 0.1, so this code will only lead to singing 10 percent of the time.
You can use the same method to apply unequal weights to multiple outcomes. Let’s say you want singing to have a 60 percent chance of happening, dancing, a 10 percent chance, and sleeping, a 30 percent chance. Again, you can pick a random number between 0 and 1 and see where it falls:
- Between 0.0 and 0.6 (60 percent) → Singing
- Between 0.6 and 0.7 (30 percent) → Dancing
- Between 0.7 and 1.0 (30 percent) → Sleeping
let num = random(1);
if (num < 0.6) {
print("Sing!");
If random number is less than 0.6
} else if (num < 0.7) {
print("Dance!");
Between 0.6 and 0.7
} else {
print("Sleep!");
}
Greater than 0.7
Now let’s apply this methodology to the random walker so it tends to move in a particular direction. Here’s an example of a Walker with the following probabilities:
- chance of moving up: 20 percent
- chance of moving down: 20 percent
- chance of moving left: 20 percent
- chance of moving right: 40 percent
Example 0.3: A Walker That Tends to Move to the Right
step() {
let r = random(1);
if (r < 0.4) {
this.x++;
A 40% chance of moving to the right!
} else if (r < 0.6) {
this.x--;
} else if (r < 0.8) {
this.y++;
} else {
this.y--;
}
}
Another common use of this technique is to control the probability of an event that you want to occur sporadically in your code. For example, let’s say you create a sketch that starts a new random walker at regular time intervals (every 100 frames). With random() you could instead assign a 1 percent chance of a new walker starting. The end result is the same (a new walker every 1 out of 100 frames on average), but the latter incorporates chance and feels more dynamic and unpredictable.
Exercise 0.3
Create a random walker with dynamic probabilities. For example, can you give it a 50 percent chance of moving in the direction of the mouse? Remember, you can use mouseX and mouseY to get the current mouse position in p5.js!
A Normal Distribution of Random Numbers
Another way to create a nonuniform distribution of random numbers is to use a normal distribution, where the numbers cluster around an average value. To see why this is useful, let’s go back to that population of simulated monkeys and assume your sketch generates a thousand Monkey objects, each with a random height value between 200 and 300 (as this is a world of monkeys that have heights between 200 and 300 pixels).
let h = random(200, 300);
Is this an accurate algorithm for creating a population of monkey heights? Think of a crowded sidewalk in New York City. Pick any person off the street and it may appear that their height is random. Nevertheless, it’s not the kind of random that random() produces by default. People’s heights aren’t uniformly distributed; there are many more people of about average height than there are very tall or very short ones. To accurately reflect this, random heights close to the mean (another word for “average”) should be more likely to be chosen, while outlying heights (very short or very tall) should be more rare.
That’s exactly how a normal distribution (sometimes called a “Gaussian distribution” after mathematician Carl Friedrich Gauss) works. A graph of this distribution, informally known as a “bell” curve, is shown in Figure 0.2.
The curve is generated by a mathematical function that defines the probability of any given value occurring as a function of the mean (often written as μ, the Greek letter mu) and standard deviation (σ, the Greek letter sigma).
In the case of height values between 200 and 300, you probably have an intuitive sense of the mean (average) as 250. However, what if I were to say that the standard deviation is 3? Or 15? What does this mean for the numbers? The graph depicted in Figure 0.2 should give you a hint. The standard deviation changes over time. When the animation begins, it shows a high peak. This is a distribution with a very low standard deviation, where the majority of the values pile up around the mean (they don’t deviate much from the standard). As the standard deviation increases, the values spread out more evenly from the average (since they’re more likely to deviate).
The numbers work out as follows: Given a population, 68 percent of the members of that population will have values in the range of one standard deviation from the mean, 95 percent within two standard deviations, and 99.7 percent within three standard deviations. Given a standard deviation of 5 pixels, only 0.3 percent of the monkey heights will be less than 235 pixels (three standard deviations below the mean of 250) or greater than 265 pixels (three standard deviations above the mean of 250). Meanwhile, 68 percent of monkey heights will be between 245 and 255 pixels.
Calculating Mean and Standard Deviation
Consider a class of ten students who receive the following scores (out of 100) on a test:
The mean is the average:
The standard deviation is calculated as the square root of the average of the squares of deviations around the mean. In other words, take the difference between the mean and each person’s grade, and square it, giving you that person's “squared deviation.” Next, calculate the average of all these values to get the average variance. Then, take the square root of the average variance, and you have the standard deviation.
| Score | Difference from Mean | Variance |
|---|---|---|
| etc. | ||
| Average Variance: |
The standard deviation is the square root of the variance: .
Luckily, to use a normal distribution of random numbers in a p5.js sketch, you don’t have to do any of these calculations manually. Instead, the randomGaussian() function takes care of the math and returns random numbers with a normal distribution.
function draw() {
let num = randomGaussian();
}
Asking for a Gaussian random number.
What next? What if, for example, the goal is to assign the x-position of a shape drawn?
By default, the randomGaussian() function returns a normal distribution of random positive and negative numbers with a mean of 0 and a standard deviation of 1. This is also known as the standard normal distribution. Often, however, these default parameters won’t work. For example, say you want to randomly assign the x-position of a shape using a normal distribution with a mean of 320 (the center horizontal pixel in a window of width 640) and a standard deviation of 60 pixels. In this case, you can adjust the parameters by passing the randomGaussian() function two arguments: the mean followed by the standard deviation.
Example 0.4: A Gaussian Distribution
function draw() {
let x = randomGaussian(320, 60);
A normal distribution with mean 320 and standard deviation 60
noStroke();
fill(0, 10);
circle(x, 120, 16);
}
Here I’ve used arguments to customize the call to randomGaussian(), but note that the math to implement this customization is quite simple: all you have to do is multiply the value from the standard normal distribution by the standard deviation and then add the mean. In other words, assigning x to randomGaussian(320, 60) is the same as the following:
let x = 60 * randomGaussian() + 320;
By drawing the circles on top of each other with transparency, you can begin to see the distribution. The darkest spot is near the center, where most of the values cluster, but every so often circles are drawn farther to the right or left of the center.
Exercise 0.4
Consider a simulation of paint splatter drawn as a collection of colored dots. Most of the paint clusters around a central position, but some dots splatter out toward the edges. Can you use a normal distribution of random numbers to generate the positions of the dots? Can you also use a normal distribution of random numbers to generate a color palette? Try creating a slider to adjust the standard deviation.
Exercise 0.5
A Gaussian random walk is defined as one in which the step size (how far the object moves in a given direction) is generated with a normal distribution. Implement this variation of the Walker class.
A Custom Distribution of Random Numbers
There will come a time in your life when you don’t want a uniform distribution of random values, or even a Gaussian one. Imagine for a moment that you’re a random walker in search of food. Moving randomly around a space seems like a reasonable strategy for finding something to eat. After all, you don’t know where the food is, so you might as well search randomly until you find it. However, there’s a problem. As you may have noticed watching your Walker object in action, random walkers return to previously visited positions many times, a phenomenon known as oversampling. This could make your search for food fruitless, or at least inefficient.
One strategy to avoid such a problem is to take a very large step every so often. This allows the walker to forage randomly around a specific position while periodically jumping very far away to reduce the amount of oversampling. This variation on the random walk, known as a Lévy flight, requires a custom set of probabilities. Though not an exact implementation of a Lévy flight, you could state the probability distribution as follows: the longer the step, the less likely it is to be picked; the shorter the step, the more likely.
Earlier I wrote that you could generate custom probability distributions by filling an array with values (some duplicated so as to be picked more frequently) or by testing the result of random(). One way to implement a Lévy flight might be to specify a 1 percent chance of the walker taking a large step.
let r = random(1);
if (r < 0.01) {
xstep = random(-100, 100);
ystep = random(-100, 100);
A 1% chance of taking a large step
} else {
xstep = random(-1, 1);
ystep = random(-1, 1);
}
However, this reduces the probabilities to a fixed number of options: 99 percent of the time, a small step; 1 percent of the time, a large step. What if you instead wanted to make a more general rule: the higher a number, the more likely it is to be picked. For example, 0.8791 would be more likely to be picked than 0.8532, even if that likelihood is just a tiny bit greater. In other words, if is the random number, the likelihood of it being picked could be mapped to the y-axis with the function (Figure 0.3).
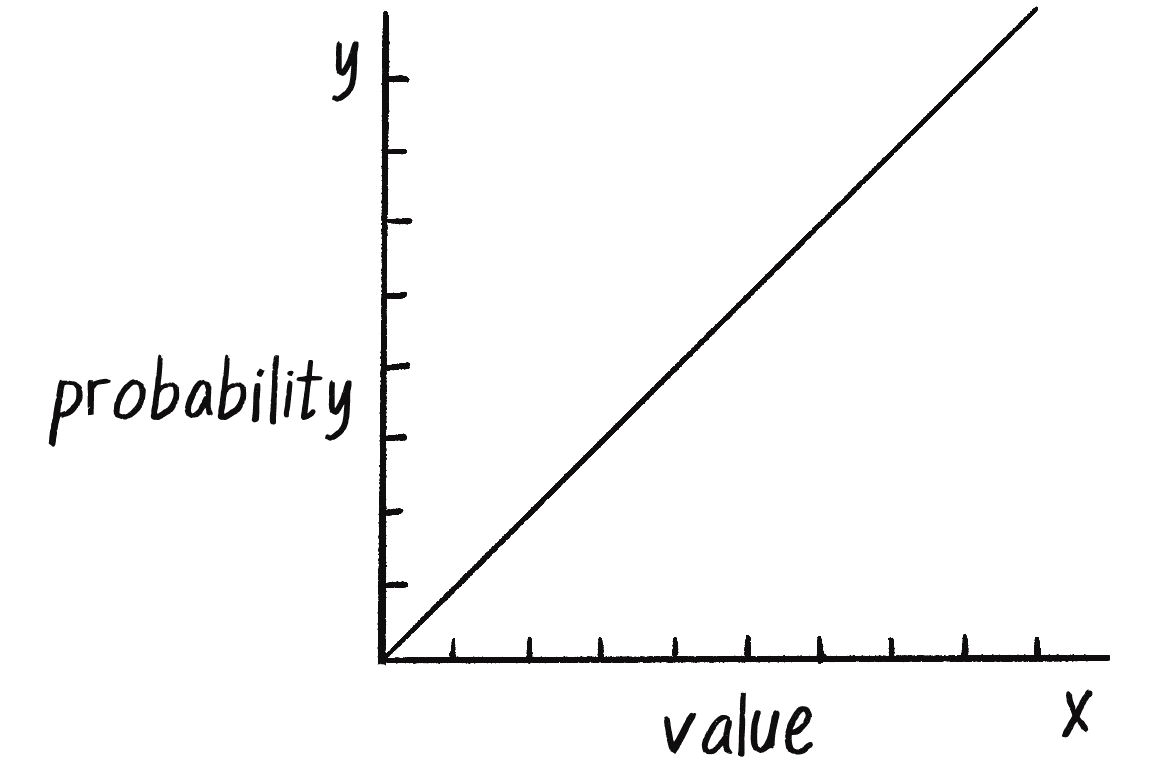
If a distribution of random numbers can be generated according to the graph in Figure 0.3, then you should also be able to generate a random distribution that follows any other curve you can define with a formula.
One solution for a custom distribution is to pick two random numbers instead of one. The first random number is just that, a random number. The second one, however, is what I’ll call a qualifying random value. It will decide whether to use that first number or throw it away and pick another. Numbers that have an easier time qualifying will be picked more often, and numbers that rarely qualify will be picked infrequently. Here are the steps (for now, I’ll consider only random values between 0 and 1):
- Pick a random number:
r1. - Compute a probability
pthatr1should qualify. Let’s try:p = r1. - Pick another random number:
r2. - If
r2is less thanp, then you’ve found your number:r1! - If
r2isn’t less thanp, go back to step 1 and start over.
Here, the likelihood that a random value will qualify is equal to the random number itself, just as you saw in Figure 0.3. If r1 equals 0.1, for example, r1 will have a 10 percent chance of qualifying. If r1 equals 0.83, it will have an 83 percent chance of qualifying. The higher the number, the greater the likelihood that it gets used.
This process is called the accept-reject algorithm, a type of Monte Carlo method (named for the Monte Carlo casino). Here’s a function that implements the accept-reject algorithm, returning a random value between 0 and 1.
Example 0.5: An Accept-Reject Distribution
function acceptreject() {
while (true) {
Do this “forever” until we find a qualifying random value.
let r1 = random(1);
Pick a random value.
let probability = r1;
Assign a probability.
let r2 = random(1);
Pick a second random value.
if (r2 < probability) {
return r1;
}
}
}
Does it qualify? If so, we’re done!
While the accept-reject algorithm does work for generating custom distributions of random numbers, it’s not a particularly efficient technique. It can lead to a considerable amount of wasted computation when a large number of random values are rejected, especially when the qualifying probability is very low. When I get to genetic algorithms in Chapter 9, I’ll take a different, more optimal approach.
Exercise 0.6
Use a custom probability distribution to vary the size of the random walker’s steps. The step size can be determined by influencing the range of values picked with a qualifying random value. Can you map the probability to a quadratic function by making the likelihood that a value is picked equal to the value squared?
let step = 10;
let stepx = random(-step, step);
let stepy = random(-step, step);
this.x += stepx;
this.y += stepy;
A uniform distribution of random step sizes. Change this!
(In Chapter 1, I’ll show how to vary the step sizes more efficiently with vectors.)
A Smoother Approach with Perlin Noise
A good random number generator produces numbers that have no relationship and show no discernible pattern. As I’ve hinted, however, while a little bit of randomness can be a good thing when programming organic, lifelike behaviors, uniform randomness as the single guiding principle isn’t necessarily natural. An algorithm known as Perlin noise, named for its inventor Ken Perlin, takes this concept into account by producing a naturally ordered sequence of pseudorandom numbers, where each number in the sequence is quite close in value to the one before it. This creates a “smooth” transition between the random numbers and a more organic appearance than pure noise, making Perlin noise well suited for generating various effects with natural qualities, such as clouds, landscapes, and patterned textures like marble.
To illustrate the difference between Perlin noise and uniform randomness, consider Figure 0.4. The graph on the left shows Perlin noise over time, with the x-axis representing time; note the smoothness of the curve. The graph on the right shows noise in the form of purely random numbers over time; the result is much more jagged. (The code for generating these graphs is available in the accompanying book downloads.)
Ken Perlin developed the original, “classic” Perlin noise algorithm while working on the movie Tron in the early 1980s; he later received an Academy Award in technical achievement for this work. The algorithm was designed to create procedural textures for computer-generated effects. (“Procedural" refers to generating the visual elements algorithmically, rather than an artist manually designing them.) Over the years, there have been a variety of other "flavors" of noise developed by different authors. Some notable ones are Value noise, Worley noise, and Simplex noise (developed by Perlin himself in 2001). You can learn more about the history of Perlin noise at Ken Perlin’s website, and its variations over the years in my "What Is OpenSimplex Noise?" video on thecodingtrain.com.
The p5.js library incorporates an implementation of the classic Perlin noise algorithm from 1983 in a function callednoise(). It can takes one, two, or three arguments, as noise is computed in one, two, or three dimensions. I’ll start by showing you one-dimensional noise.
Say you want to draw a circle on a canvas at a random x-position. Out of habit, you might use the random() function:
let x = random(0, width);
A random x-position
circle(x, 180, 16);
Now, instead of a random x-position, you want a “smoother” Perlin noise x-position. You might think that all you need to do is replace random() with an identical call to noise(), like so:
let x = random(0, width);
Replace random() with noise()?
let x = noise(0, width);
circle(x, 180, 16);
(Tempting, but this is not correct!)
Conceptually, this is exactly what you want to do—calculate an x-value that ranges between 0 and the width according to Perlin noise—but this isn’t the correct implementation. While the arguments to the random() function specify a range of values between a minimum and a maximum, noise() doesn’t work this way. Instead, its output range is fixed: it always returns a value between 0 and 1. You’ll see in a moment that you can get around this easily with p5’s map() function, but first let’s examine what exactly noise() expects you to pass in as an argument.
One-dimensional Perlin noise can be thought of as a linear sequence of values over time. For example:
| Time | Noise Value |
|---|---|
| 0 | 0.365 |
| 1 | 0.363 |
| 2 | 0.363 |
| 3 | 0.364 |
| 4 | 0.366 |
In order to access a particular noise value, you have to choose a "moment in time" and pass it to the noise() function. For example:
let n = noise(3);
According to the above table, noise(3) returns 0.364. The next step is to use a variable for time and ask for a noise value continuously in draw():
let t = 3;
function draw() {
let n = noise(t);
We need the noise value for a specific moment in time.
print(n);
}
Close, but not quite. This code just prints the same value over and over because it keeps asking for the result of the noise() function at the same point in time, 3. If the time variable t increments, however, you’ll get a different noise value each time you call the function.
let t = 0;
function draw() {
let n = noise(t);
print(n);
It's convention start with an offset of t = 0, though this is arbitrary.
t += 0.01;
}
Now, we move forward in time!
I’ve chosen to increment t by 0.01, but using a different increment value will affect the smoothness of the noise. Larger jumps in time that skip ahead through the noise space produce values that are less smooth, and more random (Figure 0.5).
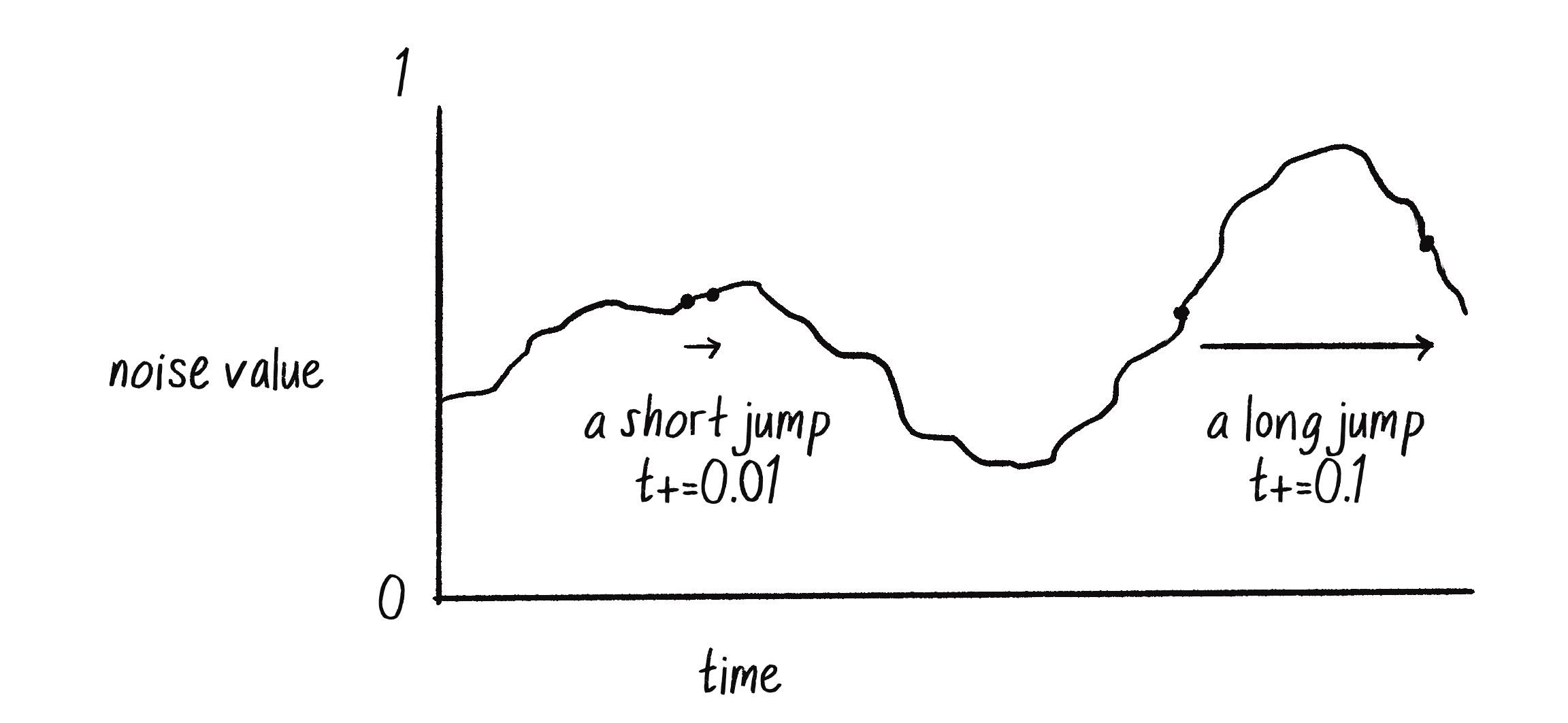
In the upcoming code examples that utilize Perlin noise, pay attention to how the animation changes with varying values of t.
Noise Ranges
Once you have noise values that range between 0 and 1, it’s up to you to map that range to whatever size suits your purpose. The easiest way to do this is with p5’s map() function (Figure 0.6). It takes five arguments. First is the value you want to map, in this case n. This is followed by the value’s current range (minimum and maximum), followed by the desired range.
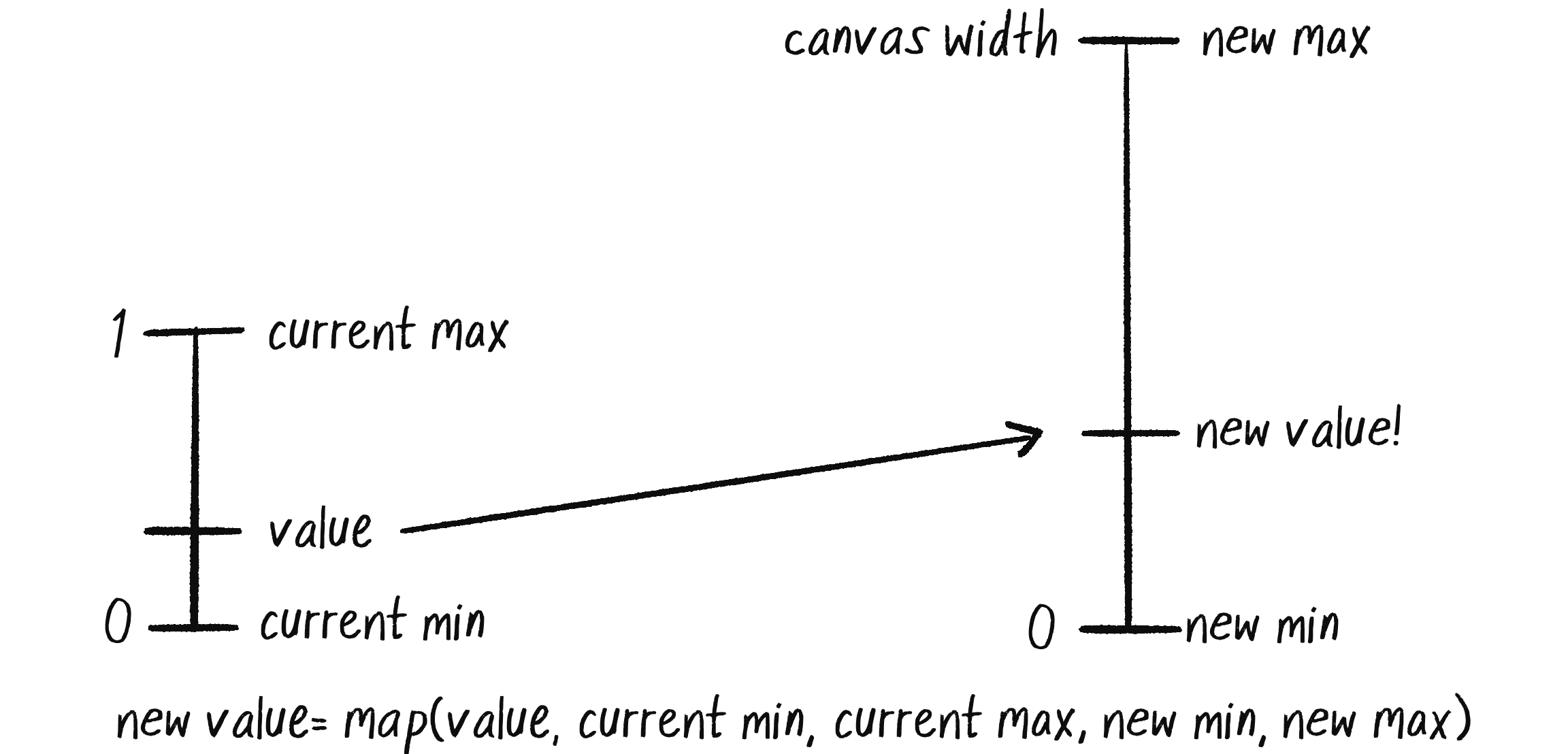
In this case, while noise has a range between 0 and 1, I’d like to draw a circle with an x-position ranging between 0 and the canvas’s width.
let t = 0;
function draw() {
let n = noise(t);
let x = map(n, 0, 1, 0, width);
Using map() to customize the range of Perlin noise
ellipse(x, 180, 16, 16);
t += 0.01;
}
The exact same logic can be applied to the random walker, assigning both its x- and y-values according to Perlin noise. This creates a smoother, more organic random walk.
Example 0.6: A Perlin Noise Walker
class Walker {
constructor() {
this.tx = 0;
this.ty = 10000;
}
step() {
this.x = map(noise(this.tx), 0, 1, 0, width);
this.y = map(noise(this.ty), 0, 1, 0, height);
x- and y-position mapped from noise
this.tx += 0.01;
this.ty += 0.01;
}
}
Move forward through “time.”
Notice how this example requires a new pair of variables: tx and ty. This is because we need to keep track of two time variables, one for the x-position of the Walker object and one for the y-position. But there’s something a bit odd about these variables. Why does tx start at 0 and ty at 10,000? While these numbers are arbitrary choices, I’ve intentionally initialized the two time variables this way because the noise function is deterministic: it gives you the same result for a specific time t each and every time. If I asked for the noise value at the same time t for both x and y, then x and y would always be equal, meaning that the Walker object would only move along a diagonal. Instead, I use two different parts of the noise space, starting at 0 for x and 10,000 for y, so that x and y appear to act independently of each other (Figure 0.7).

In truth, there’s no actual concept of time at play here. It’s a useful metaphor to help describe how the noise function works, but really what you have is space, rather than time. The graph in Figure 0.7 depicts a linear sequence of noise values in a one-dimensional space—that is, arranged along a line. Values are retrieved at a specific x-position which is why you’ll often see a variable named xoff in examples to indicate the x-offset along the noise graph, rather than t for time.
Exercise 0.7
In the Perlin noise random walker, the result of the noise function is mapped directly to the walker’s position. Create a random walker where you instead map the result of the noise() function to the walker’s step size.
Two-Dimensional Noise
Having explored the concept of noise values in one dimension, let's consider how they can also exist in a two-dimensional space. With one-dimensional noise, there’s a sequence of values in which any given value is similar to its neighbor. Imagine a piece of graph paper (or a spreadsheet!) with the values for 1D noise written across a single row, one value per cell. Because these values live in one dimension, each has only two neighbors: a value that comes before it (to the left) and one that comes after it (to the right), as shown on the left in Figure 0.8.
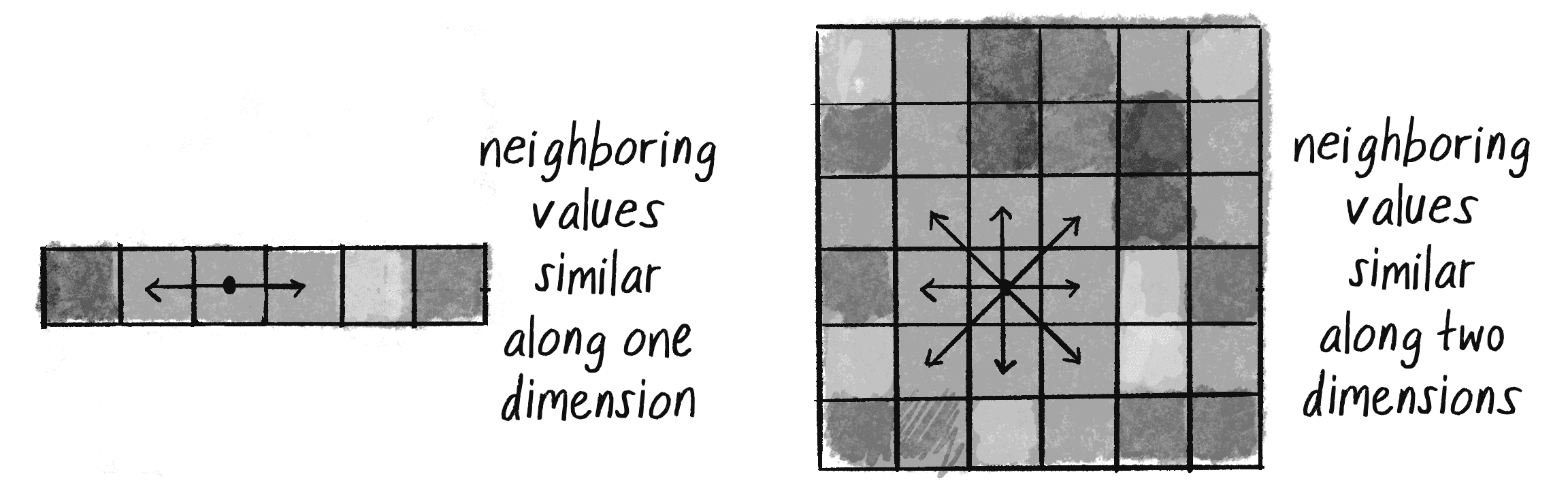
Two-dimensional noise works exactly the same way conceptually. The difference, of course, is that the values aren’t just written in a linear path along one row of the graph paper, but rather fill the whole grid. A given value will be similar to all of its neighbors: above, below, to the right, to the left, and along any diagonal, as in the right half of Figure 0.8.
If you were to visualize this graph paper with each value mapped to the brightness of a color, you would get something that looks like clouds. White sits next to light gray, which sits next to gray, which sits next to dark gray, which sits next to black, which sits next to dark gray, and so on.
This is why noise was originally invented. If you tweak the parameters and play with color, the resulting images look more like marble, wood, or any other organic texture.
Noise Detail
The p5.js noise reference explains that noise is calculated over several “octaves.” Calling the noiseDetail() function changes both the number of octaves and their importance relative to one another. This, in turn, changes the quality of the noise values produced.
If you wanted to color every pixel of a canvas randomly using the random() function, you would need a nested loop to cycle through the rows and columns of pixels and pick a random brightness for each. (Note that in p5, the pixels are arranged in an array with four spots for each: red, green, blue, and alpha. For details, see the pixel array video tutorial in the "p5 Tips and Tricks" track at thecodingtrain.com).
loadPixels();
for (let x = 0; x < width; x++) {
for (let y = 0; y < height; y++) {
let index = (x + y * width) * 4;
let bright = random(255);
A random brightness!
pixels[index ] = bright;
pixels[index + 1] = bright;
pixels[index + 2] = bright;
Setting the red, green, and blue values
pixels[index + 3] = 255;
}
}
updatePixels();
Set alpha of 255 (no transparency).
To color each pixel more smoothly according to the noise() function, you can do exactly the same thing, only instead of calling random() you’ll call noise().
let bright = map(noise(x, y), 0, 1, 0, 255);
A Perlin noise brightness!
This is a nice start conceptually—it gives you a noise value for every position in a two-dimensional space. The problem is that this won’t have the smooth, cloudy quality you want. Incrementing by 1 through the noise space from one pixel to the next is too large a jump. Remember, with one-dimensional noise, I incremented the time variable by 0.01 each frame, not by 1!
A pretty good solution to this problem is to just use different variables for the noise arguments than you’re using to access the pixels on the canvas. For example, you can increment a variable called xoff by 0.01 each time x increases horizontally by 1, and a yoff variable by 0.01 each time y increases vertically by 1 through the nested loops.
let xoff = 0.0;
for (let x = 0; x < width; x++) {
Start xoff at 0.
let yoff = 0.0;
for (let y = 0; y < height; y++) {
For every xoff, start yoff at 0.
let bright = map(noise(xoff, yoff), 0, 1, 0, 255);
Use xoff and yoff for noise().
let index = (x + y * width) * 4;
Use x and y for pixel position.
pixels[index] = bright;
pixels[index + 1] = bright;
pixels[index + 2] = bright;
pixels[index + 3] = 255;
Setting the red, green, blue, alpha values
yoff += 0.01;
}
Increment yoff.
xoff += 0.01;
}
Increment xoff.
I have to confess, I've done something rather confusing. I've used one-dimensional noise to set two variables (this.x and this.y) controlling the 2D motion of a walker. Then, I promptly moved on to using two-dimensional noise to set one variable (bright) controlling the brightness of each pixel in the canvas. The key difference here is that for the walker, my goal is to have two independent one-dimensional noise values; it’s just a coincidence that I’m using them to move an object through two-dimensional space. The way to accomplish this is to use two different offsets (this.tx and this.ty) to pull values from different parts of the same one-dimensional noise space. Meanwhile, in the 2D noise example, both xoff and yoff start at 0 because I'm just looking for a single value (a pixel brightness) for a given point in a two-dimensional noise space. The walker is actually navigating two separate one-dimensional noise paths, whereas the pixels are single values in a two-dimensional space.
Exercise 0.8
Play with color, noiseDetail(), and the rate at which xoff and yoff are incremented to achieve different visual effects.
Exercise 0.9
Add a third argument to noise that increments once per cycle through draw() to animate the two-dimensional noise.
Exercise 0.10
Use the noise values as the elevations of a landscape.
I’ve suggested several traditional uses of Perlin noise in this section. I assigned the smooth values of one-dimensional noise to the position of an object to give the appearance of wandering. With two-dimensional noise, I generated a cloudy pattern using smoothed values on a plane of pixels. It’s important to remember, however, that Perlin noise values are just that—values. They aren’t inherently tied to pixel positions or color. Any example in this book that has a variable could be controlled via Perlin noise. When I model a wind force, for instance, its strength could be controlled by Perlin noise. Same goes for the angles between the branches in a fractal tree pattern, or the speed and direction of objects moving along a grid in a flow field simulation (see Figure 0.9).
The Ecosystem Project
As mentioned in the Introduction, one way to use this book is to build a single project over the course of reading it, incorporating elements from each chapter as you go. One idea for this is a simulation of an ecosystem. Imagine a population of computational creatures swimming around a digital pond, interacting with each other according to various rules.
Step 0 Exercise:
Develop a set of rules for simulating the real-world behavior of a creature, building on top of principles from the “random walk” or other noise-driven motions. Can you simulate a jittery bug that flies in unpredictable ways, or perhaps a floating leaf carried by an inconsistent breeze? Start by exploring the boundaries of how much you can express a creature’s personality through its behavior before focusing on its visual characteristics.
Here's an illustration to help you generate ideas for building an ecosystem based on the topics covered in this book. Watch how the illustration evolves as new concepts and techniques are introduced with each subsequent chapter. The goal of this book is to demonstrate algorithms and behaviors, so my examples will almost always only include a single primitive shape, such as a circle. However, I fully expect that there are creative sparks within you, and encourage you to challenge yourself with the designs of the elements you draw on the canvas. If drawing with code is new to you, the book's illustrator, Zannah Marsh, has written a helpful guide that you can find in the book’s Appendix.
Onward
I’ve talked in this chapter about how it’s easy to rely too much on randomness. In many ways, it’s the most obvious answer to the kinds of questions we ask continuously: How should this object move? What color should it be? This obvious answer, however, is sometimes a lazy one.
As I finish this chapter, it’s also worth noting that you could just as easily fall into the trap of overusing Perlin noise. How should this object move? Perlin noise! What color should it be? Perlin noise! How fast should it grow? Perlin noise!
The point of all of this is not to say that you should or shouldn’t use randomness. Or that you should or shouldn’t use Perlin noise. The point is that the rules of your system are yours to define. The larger your programming toolbox, the more choices you’ll have as you implement those rules. If all you know is randomness, then your design thinking is limited. Sure, Perlin noise helps, but you’ll need more. A lot more. The goal of this book is to fill your toolbox, so you can make more informed choices and design more thoughtful systems.
class Walker {